Regra de 3 no Excel: Como Calcular?
Quer aprender a calcular a Regra de 3 no Excel? Então você está no lugar certo!
A regra de três é provavelmente uma das operações matemáticas “informais” mais amplamente utilizadas. Comumente aprendida quando estamos na escola, essa operação tem muitas utilidades também em nossa vida cotidiana.
Mas e você, sabe como calculá-la utilizando o Excel? Confira os detalhes a seguir e veja como é fácil!
Navegue pelo tópico de seu interesse:
O que é Regra de 3?
A regra de três é uma técnica usada para encontrar uma medida quando conhecemos outras três, desde que essas quatro medidas formem uma proporção.
Para melhor compreensão sobre este assunto, suponha que uma fábrica consiga produzir 100 peças diárias de um produto com apenas 5 funcionários. Neste caso, quantos funcionários são necessários para produzir 400 peças diárias?
Para resolver este tipo de problema, usamos a regra de três. Então, note que existem duas grandezas proporcionais no problema, uma é a quantidade de funcionários e outra a quantidade de peças diárias. Observe também que são conhecidas três medidas dessas grandezas e queremos descobrir a quarta medida. E é por isso que essa técnica é conhecida como regra de três.
Então, construindo a proporção relativa a esse problema, temos:
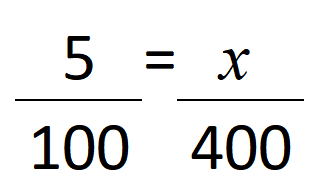
Para encontrar o valor de x, basta utilizar os conhecimentos provenientes das equações ou usar a propriedade fundamental das proporções: o produto dos extremos é igual ao produto dos meios. Essa propriedade também é conhecida como “multiplicação cruzada”. Para aplicá-la, basta multiplicar 100 por x e 5 por 400
Deste modo, resolvendo essa equação, temos:
100x = 2000
x = 2000/100
x = 20
Ou seja, serão necessários 20 funcionários para produzir 400 produtos por dia.
Isso significa que aumentando o número de funcionários, aumentamos também o número de produtos produzidos por dia. E quando duas grandezas possuem essa propriedade, elas são chamadas de grandezas diretamente proporcionais. Sempre que duas grandezas são diretamente proporcionais, o cálculo da regra de três poderá ser feito desta maneira.
Por outro lado, quando aumentamos a medida relativa a uma grandeza e a outra diminui por consequência disso, as grandezas são ditas inversamente proporcionais.
Para entender como isso funciona, suponha que um trem se move a 50 km/h e leva 2 horas para chegar ao seu destino. Quanto tempo esse mesmo trem levaria se estivesse a 100 km/h?.
Observe que aumentando a velocidade, o tempo gasto no percurso diminui, portanto, essas grandezas são inversamente proporcionais. Nesse caso, devemos construir a proporção colocando a velocidade em uma fração e o tempo na outra.
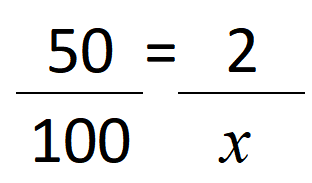
E como são grandezas inversamente proporcionais, antes de aplicar a propriedade fundamental das proporções, é necessário inverter uma das frações. Então, aplicando a propriedade, temos:
100x = 2*50
100x = 100
x = 100/100
x = 1
Portanto, o trem gastará apenas 1 hora no percurso se estiver a 100Km/h
Como Calcular Regra de 3 no Excel
Agora que você já conhece os conceitos básicos da regra de 3, vamos conferir como que fica esse cálculo no Excel.
Diretamente Proporcional
Utilizando o primeiro exemplo que foi citado anteriormente, observe que organizamos as quantidades de funcionários de um lado e a quantidade de produtos fabricados do outro.
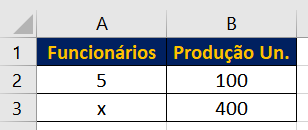
Deste modo, como se trata de um problema diretamente proporcional (ou seja, quanto mais funcionários, maior a produção) vamos utilizar a multiplicação cruzada.
=A2*B3/B2
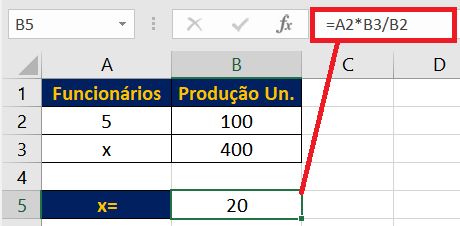
Ou seja, A2*B3 é o produto de 5*400, que representa uma das multiplicações cruzadas. Ao dividirmos tal resultado por B2, estamos isolando a variável x, visto que A3 é a célula que acompanharia o x na outra multiplicação cruzada.
Sendo assim, para o cálculo de regra de três no Excel, faça a multiplicação cruzada que não envolve a variável que deseja conhecer e divida pelo outro elemento da outra multiplicação cruzada, que não é o x.
Inversamente Proporcional
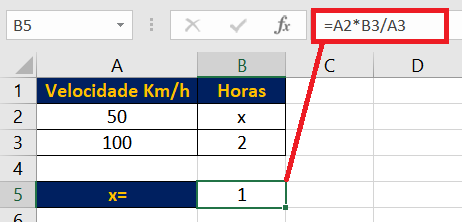
Por outro lado, utilizando o segundo exemplo citado anteriormente, temos que quanto maior a velocidade do trem, menor será o tempo da viagem. Portanto, temos uma regra de 3 inversamente proporcional.
Então observe que inserimos de um lado a velocidade do trem e do outro lado o tempo de viagem.
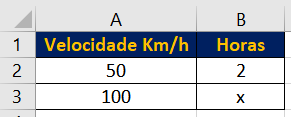
Em seguida, invertemos uma das frações e utilizamos a fórmula conforme demonstrado anteriormente. Ou seja:
=A2*B3/A3
Regra de 3 Composta
Conforme mencionado anteriormente, a regra de três é um cálculo matemático para a resolução de diversos problemas que envolvem duas ou mais grandezas diretamente ou inversamente proporcionais.
Nos exemplos anteriores, utilizamos cenários que envolviam apenas duas grandezas diretamente ou inversamente proporcionais. E para esses casos, podemos classificar com Regra de 3 Simples.
Por outro lado, quando temos mais de duas grandezas relacionadas entre si, direta ou inversamente, então podemos classificar como Regra de 3 Composta.
Para melhor compreensão, observe os exemplo abaixo:
Regra de 3 Composta Diretamente Proporcional
Sabe-se que cinco garrafas de água de 2 litros pesam 10 quilos. Quanto pesam duas garrafas de 3 litros?
Note que temos 3 grandezas nesse problema, que são:
- Garrafas
- Litros
- Quilos
A relação entre elas é:
5 garrafas, 2 litros, 10 quilos
2 garrafas, 3 litros, X quilos

Agora precisamos trabalhar a relação entre as grandezas, sempre comparando com a grandeza onde a incógnita é X.
Comparando garrafas com quilos: Se houver menos garrafas, elas pesarão menos. Portanto, há uma proporcionalidade direta.
Comparando litros com quilos: Se houver mais litros, eles pesarão mais. Novamente, há uma proporcionalidade direta.
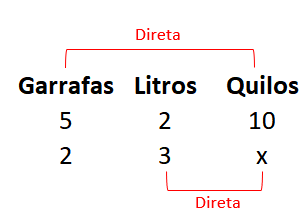
Agora escrevemos as relações na forma de uma fração para poder encontrar a incógnita X. A primeira fração inclui a incógnita (isso não é obrigatório, mas ajudará a resolvê-la mais tarde). Em seguida, representamos a multiplicação das duas frações como uma equação.
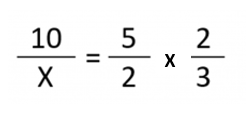
E resolvemos:
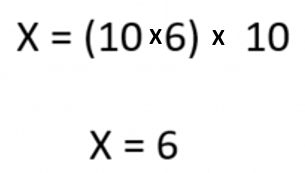
Duas garrafas de 3 litros pesam 6 quilos.
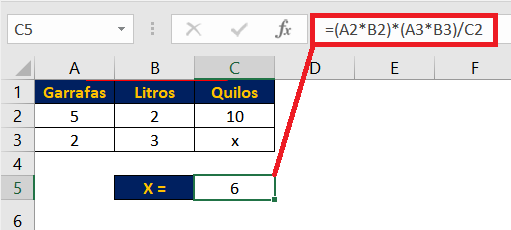
Para calcular a Regra de 3 Composta Inversamente Proporcional no Excel a fórmula ficará da seguinte maneira:
=(A2*B2)*(A3*B3)/C2
Regra de 3 Composta Inversamente Proporcional
6 impressoras imprimiram 100 livros em 4 dias. Quantos dias serão necessários para imprimir 50 livros se tivermos 4 impressoras?
Note que temos 3 grandezas nesse problema, que são:
- Impressoras
- Livros
- Dias
A relação entre elas é:
4 dias, 6 impressoras, 100 livros.
X dias, 4 impressoras, 50 livros.

Observe que se precisamos imprimir menos livros, precisamos, portanto, de menos dias. Proporcionalidade direta.
Se houver menos impressoras, precisamos de mais dias = proporcionalidade inversa.

Agora precisamos escrever as relações na forma de fração, para podermos encontrar a incógnita X. Mas antes, precisamos inverter a grandeza inversa, portanto, o denominador se torna o numerador e o numerador se torna o denominador.
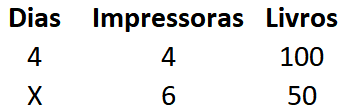
Em seguida, podemos resolver o problema da mesma forma que os anteriores, usando o método de multiplicação cruzada.
X = (4*6*50) / (4*100)
X = 1200 / 400
X= 3
4 impressoras levam 3 dias para imprimir 50 livros.
Para calcular a Regra de 3 Composta Inversamente Proporcional no Excel, o processo é praticamente o mesmo. Ou seja, basta organizar as grandezas em suas respectivas células e inverter as frações onde a grandeza é inversamente proporcional. Veja o exemplo abaixo para melhor compressão.
=(B3*C3)/(B2*C2)*A2
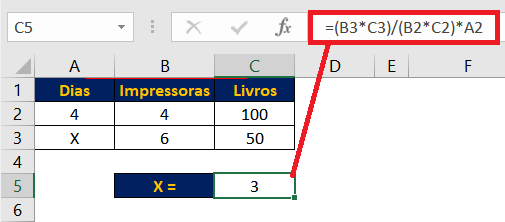
Baixe aqui a planilha com os exemplos apresentados neste tutorial
Confira também as seguintes dicas de Excel:
- Porcentagem no Excel | Como Calcular?
- Mediana no Excel: Como Calcular?
- Raiz Quadrada no Excel: Como calcular?
- Potenciação no Excel: 2 Métodos Para Você Calcular
E então, o que achou da dica para calcular Regra de 3 no Excel? Caso tenha ficado com alguma dúvida, basta deixar o seu comentário abaixo!